繰り上がり・繰り下がりができない理由

繰り上がり・繰り下がりの困難は、別々の問題ではなく『数概念(サビタイジング)』の欠如という一つの原因に集約されます。当サイトでは、これらを一つの論理で一貫して解決する、独自の体系的メソッドを提示します。
この問題を解決するキーワードが「subitizing(サビタイジング)」であることは、「なぜ計算ができないのか」のページでご説明いたしました。
繰り上がりができないという問題を解決するキーワードも、同じくsubitizing、より詳しくは「subitizingの組み合わせ」が関係します。
Subitizingの組み合わせとは?
1992年、科学ジャーナル『Nature』にて、生後5か月の赤ちゃんがsubitizingtができるだけでなく、1+1=2 や 2-1=1 等の単純な計算も理解しているという論文が発表されました。
言語を理解できない赤ちゃんが計算を理解している。これは、人間が生まれながらに持つ数認知能力「subitizing」を、単体ではなく組み合わせでも認知できることを意味します。
大人がsubitizingできる範囲は5までですが、例えば「6」という数は、「1」のsubitizingと「5」のsubitizingの組み合わせとして認知していると考えられます。この考え方は、古代文明の記数法にも見られます。

このように、subitizingの範囲は5までですが、組み合わせることにより5より大きい数も直感的に認知できるのです。
2~10までの数をsubitizingの組み合わせで表現すると、以下のようになります。
3.jpg)
この考え方に立つと、計算とは「subitizingの組み合わせを変化させること」と捉えることができます。
なぜ繰り上がり・繰り下がりができないのか
ここで、繰り上がりのある「8+3」の計算を考察します。一般的な指導法(さくらんぼ計算など)では、「10の補数(あといくつで10になるか)」を考え、数を分解して計算します。しかし、算数の苦手な子は、まずこの説明自体が理解できません。
指導の目的は「補数」という考え方を習得させることですが、苦手な子は「数え上げ(カウンティング)」で乗り切ろうとします。ここに繰り上がりができない根本的な原因があるのです。
これを解決するためには、カウンティングではなく、人が生まれつき持っているsubitizingを使うように指導すればいいのです。
色そろばんによる解決策
色そろばんには、このsubitizingの組み合わせを簡単に表現できる仕組みがあり、使うことにより簡単に繰り上がり・繰り下がりも計算できてしまいます。
下図の仕組みにより、すべての数をsubitizingの組み合わせで認知できるようになります。

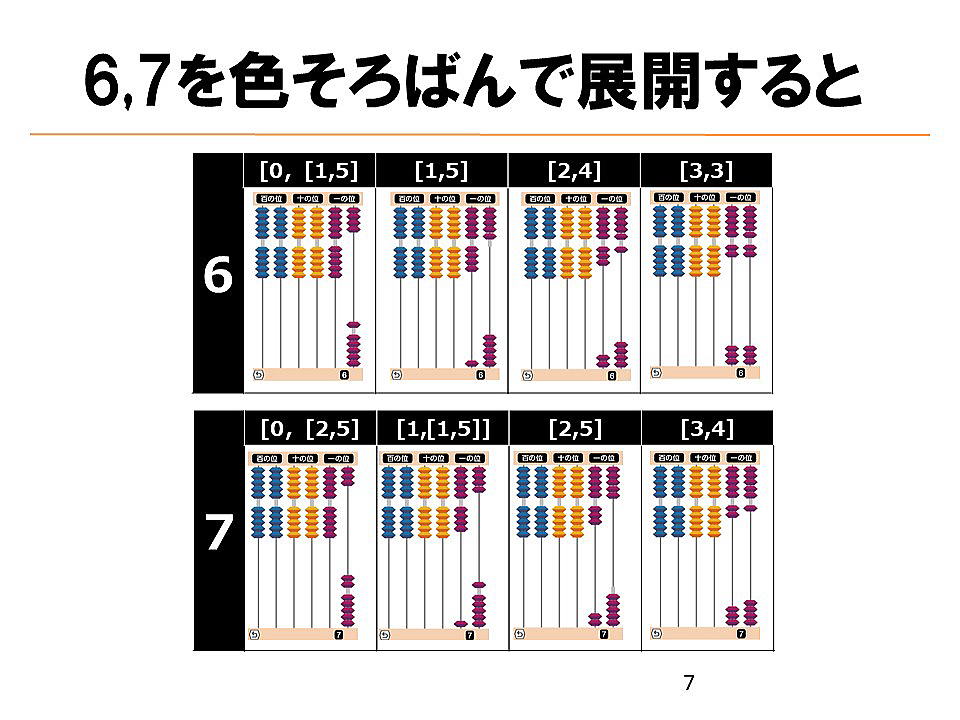
繰り上がりの足し算も、下図のようにsubitizingの組み合わせとして簡単に計算できます。

学習用動画で確認すると、より容易に理解できるでしょう。
2位数+2位数(繰り上がりが2回あり)の足し算も、色そろばんを使えば動画のように簡単にできてしまいます。
繰り下がりでよくある「17-8=11」のような間違い(引けないから大きい方から引いてしまう)も、色そろばんで学習すれば簡単にわかります。

「102-3」,「655-457」等、3位数の繰り下がりがある引き算も、色そろばんを使えば簡単にできてしまいます。↓の動画をご覧ください
既存の指導法との比較
補数を学習する必要はない
繰り上がりの計算では補数を学びますが、計算が苦手な子は結局カウンティングで答えを探し、文章問題の意味が理解できなければ先に進めません。色そろばんではこの学習は不要です。難しい補数の勉強はやめましょう。補数は色そろばんの操作を体験することにより自然に理解できるからです。
さくらんぼ計算も必要ない
一般的な指導法では、補数を見つけた後に数を分解して10の塊を作りますが、手数が増え混乱の原因になります。色そろばんでは簡単な玉の操作だけで完結するため、さくらんぼ計算は必要ありません。
減加法を学習する必要はない
繰り下がりの引き算で使われる減加法は、「引き算なのになぜ足し算するの?」という疑問を生みやすく、子どもを混乱させます。色そろばんでは面倒なステップは不要で、subitizingできる数で玉を見ていくだけなので、足す操作も補数を見つける操作も必要ありません。
でも、色そろばんで「筆算」を見ると、意味が非常にクリアになる。
色そろばんは新しい指導方法です。既存の指導方法で色そろばんを使うと色そろばん本来の効果が薄れます。しかし、現行の指導方法を、色そろばんで見ることにより、その意味をを明らかにすることができます。色そろばんはsubitizingの組み合わせを変化させるという認知レベルでの学習を可能にさせているからできるのです。認知レベルで筆算を見てみましょう。
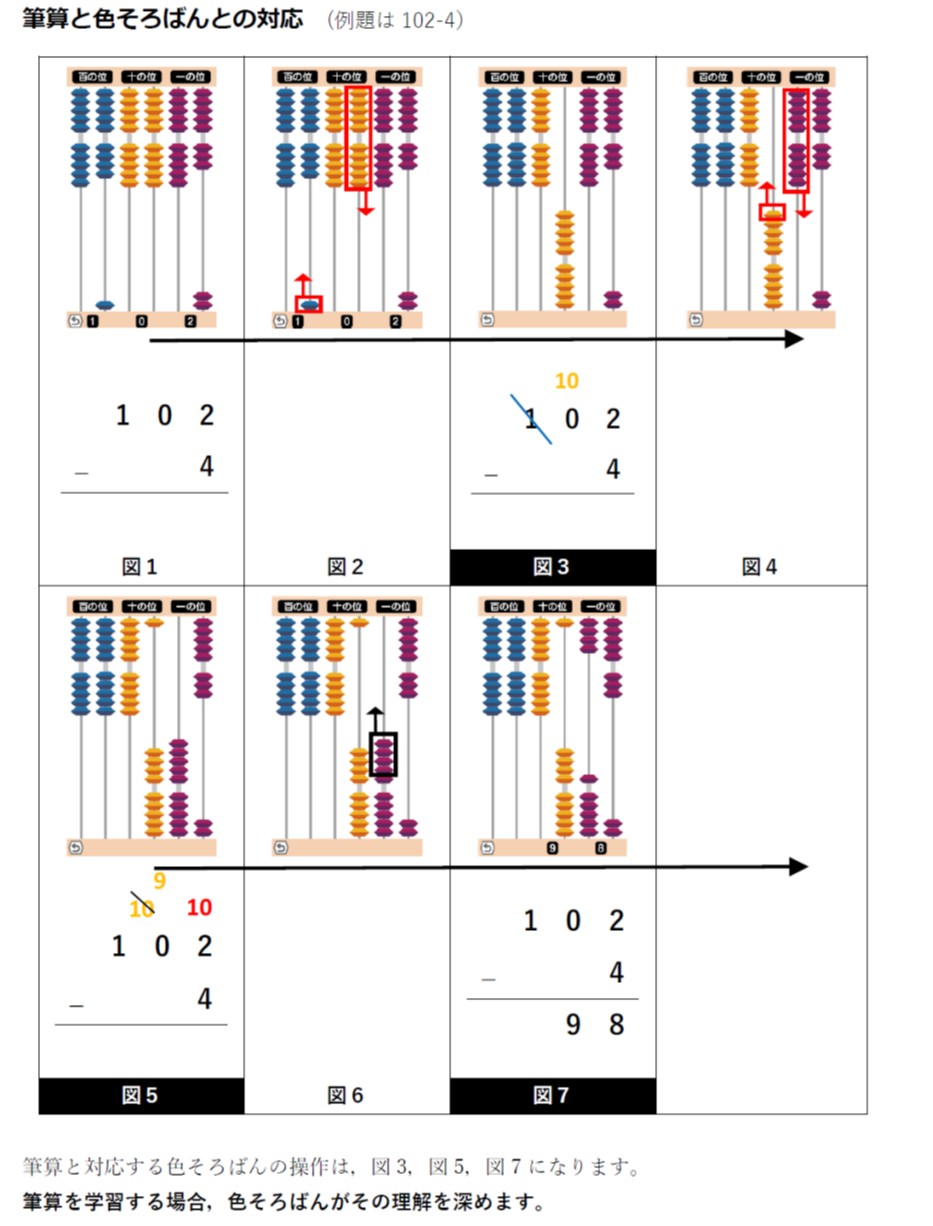
ご覧のように色そろばんの学習で求められるのは,人が本来持っているsubitizingだけです。文を理解する能力は必要ありません。また,補数を求めるように,物事を逆に考える必要もありません。だから,誰でも計算ができるようになるのです。つまり,色そろばんの玉の動きは十進法の思考そのものを表しており,この具体物に習熟することにより抽象的な十進法の思考が頭の中に自然にできるのです。計算が嫌いになるわけがないのです。
色そろばんの効果 事例紹介
多くの指導事例のうちの一部を紹介いたします。数感覚に基づいた暗算ができるようになるので,割り算,小数,分数への進むことができています。
Aさん
指導前は指を使っても計算を間違っていましたが、指導後は色そろばんを使わずに3桁の足し算・引き算を暗算で計算できました。
指導前
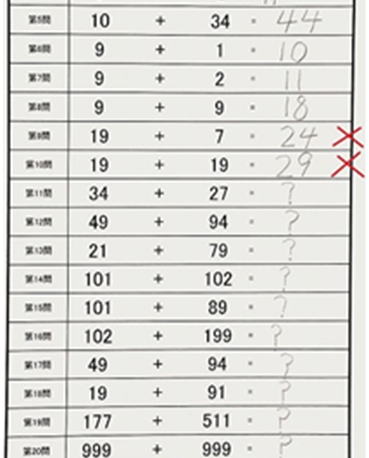
指導後

関連情報
この記事の著者:渡部 敬(わたなべ けい)
色そろばん発明者 / 第14回 辰野千壽教育賞 優秀賞受賞
10年以上にわたる教育現場での実践に基づき、計算指導の画期的な新しい方法である「色そろばん」とその理論を発明。
【文科省研究事業】
文部科学省「特別支援教育に関する実践研究充実事業」2019, 2021, 2022において研究実践が採用・掲載。算数学習に困難を抱える児童生徒への有効な指導法として、公的な教育データベースに記録されています。
【国立大学からの表彰】
国立大学法人上越教育大学より「第14回 辰野千壽教育賞」優秀賞を受賞。サビタイジング理論を応用した独自の指導体系は、教育実践研究の典型として高く評価されています。

第14回辰野千壽教育賞 優秀賞 授与式にて。中央が発明者の渡部敬