計算ができない・暗算ができない理由

上の画像は、IQ=78でADHD、学習障害のある中学1年生男子の事例です。色そろばんでの学習期間は1年半でした。指導前(計算ができない)と指導後(計算ができる)の実際の変化を示しています。
なぜ,算数ができないのか,なぜ,計算ができないのか。これは,計算が苦手であり,計算をもっとできるようになりたい。という問題と似ています。
計算がある程度できるけど,もっと早く計算できるようになりたいという方にとっては,例えば102×98の計算では,102×98=(100+2)(100-2)=1002-22 =10000-4=9996と計算する知識は非常に有用なものです。筆算なんか必要ありません。
しかし,計算ができない・暗算ができないという問題は,このようなことではありません。そもそも,計算するときは指を使ってしまい,2+3程度の簡単な計算は簡単にできるが,11-7,23+19等の計算を暗算できず,その結果これ以降の算数が全く分からないということです。また,簡単な暗算ができないため,お金の計算ができないことは社会生活に大きな影響を及ぼします。
近年,発達障害,学習障害,計算障害,算数障害,知的障害に関する議論が盛んです。計算ができない原因を障害に求めることもできます。これが一般的でしょう。
しかし,障害がなくても計算ができない方は大人の方でも結構いらっしゃいます。小学生でもたくさんいます。なぜ,できないのでしょうか。
数の2つの性質:「序数性」と「基数性」
あなたは,赤ちゃんの時,両親にお風呂に入れてもらいました。3才位になるとお風呂に入っているときは,「1つ,2つ,3つ・・・」と数えてもらったことがあるでしょう。数に接する最初の場面です。
この「1つ,2つ,3つ・・・」は,順番を表すことを目的として使っています。計算することは目的ではありません。順番を「1つ,2つ,3つ,・・・」と言葉で言っていき,「とお」もしくは「じゅう」になったときお風呂から上がったと思います。この「1つ,2つ,3つ・・」の順番を表す性質を,数の序数性といいます。
そして,しばらくすると,2つのリンゴ,2つのアイス等,数字の意味が「量」を表すことを学び,さらには,3個チョコがあったけど1個食べたから残りは2個等,今まで話してきた「1つ,2つ,3つ・・・」は単なる順番を表すのではななく,計算の対象になることを学びます。この様な数の性質を数の基数性といいます。
計算がわからなくなるのは,ほとんどの方は,3才位のお風呂に入っている「1つ,2つ,3つ・・・」からではなく,数が計算の対象となり始めたときからがほとんどです。つまり,数の性質に基数性が出てくるときにわからなくなるのです。
ここから,なぜ計算ができないのかを考えるときは,数の序数的性質と基数的性質の違いをより深く考える必要があることが分かります。今この時点で,分かることは,序数性は学習者が使用している言語に大きく依存しますが,基数性は言語環境にはほとんど依存しません。なぜなら,数を数えるとき日本語では「いち,に,さん・・」と表現しますが英語では「one,two,three・・・」で異なります。しかし,「3-2=1」は世界共通です。翻訳の必要はありません。
生まれ持った「量」を捉える能力
人が数を学習するとき,序数的性質と基数的性質のうち,どちらを先に学ぶのでしょう?
もちろん,我々の経験を思い出せば,序数的性質です。「ひとつ,ふたつ・・・」と日常生活で学びました。計算はその後で学ぶので基数的性質はその後で学びます。また,序数的性質を身につけずに基数的性質を学べるはずがありません。我々は学校でもそのように教えられてきました。
と言いたいところですが,実はそうとも言い切れないのです。
どうやら,人は,生まれながらにて,ある程度の数の量は把握できるのです。これは,1980~1990年代に行われた多くの幼児の数的能力に関する実験で証明されています。さらには,1992年の科学雑誌ネイチャーでは,生後5ヶ月の幼児に簡単な加法減法の能力があることが示されたのです。
この能力は一目で数を把握する能力であり,subitizing(サビタイジング)と言います。
幼児は3まで,大人は4,5まで,一瞬で把握できます。数えません。
さて,subitizingは序数的性質でしょうか,基数的性質でしょうか。
もちろん,基数的性質に関係する能力です。

ここで疑問が生じます。数の序数的性質を学んでから身に着けるべき基数的性質が生まれながらに身についているのか? そもそも,言葉を学ぶ以前からそのような能力を身に着けているのか?
実は,言葉を学ぶ以前から身に着けているのです。subitizingは動物にもある能力なのです。動物にもsubitizingがあるということは,ある意味納得いきます。それは,襲ってくる敵が,1匹か,2匹か,3匹か瞬時に区別できなければ,どのように逃げるべきかを判断できず,食べられていしまうからです。
古代文明に見るサビタイジングの証拠
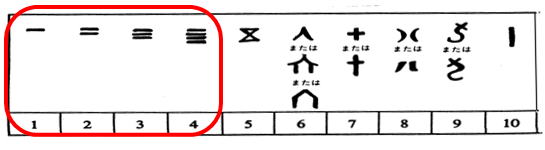
ここで,1つ面白い事実を紹介いたします。古代文明での記数法(その文明の数字)です。時間も空間が違うのに,subitizingの視点から見てみると,記数法は似た様式なのです。
古代中国式記数法
マヤ人の記数法

リキュア人の記数法

アラム人の記数法

(1988ジョルジュイフラー:数字の歴史-人類は数をどのように数えてきたか) より引用
それぞれの古代文明の数字では1から4までは点又は棒などの積み重ねで,5以降から5を表す記号を加えて数字を表しています。(中国式古代文明を除く)
なぜこのように似た様式になるのでしょうか。それは,人間はsubitizingという能力を持っているからです。その能力を使って数字を作ろうとしているからです。また,意識的に使っているのではなく自然に使っていることも読み取れます。知らないうちに似てしまっているからです。
以上の事実から,subitizingは数の基数的性質にとって非常に重要であるということが分かります。
ここで,あなた自身のsubitizingを確認してみましょう。
いくつありますか

いくつありますか

いくつありますか

いくつありますか

いくつありますか

いくつありますか

いくつありますか

いくつありますか
最初の14と次の8は数えましたね。でも,次の4,5,2,4,3,1は数えないで見ただけで一瞬で答えることができました。これがsubitizingです。あなたにもあるのです。
解決へのアプローチ
さて,問題を元に戻しましょう。なぜ計算ができないのか。計算ができないのは,数の基数的性質に関する問題であり,基数的性質にはsubitizingが大きく関係することが分かりました。そうすると,計算ができないということは,subitizngをうまく使えないから計算ができないのではないかという仮説を作ることができます。
では,どのようにすれば,学習者が自然にsubitizingをうまく使って計算できるような仕組みを作ればいいのでしょうか?
よく目につくのは,例えば,7個のおはじきがあるときは,5個の塊と,2個の塊に分けて表現しているケースです。小学校の教科書などではこのように表現している場合が多いです。
しかし,58+79等は,どのようにすればいいのでしょうか?
それには,学習者が持っているsubitizingを無意識に使えるような環境を作ることが必要です。
では,どうすればいいのでしょうか?
ここをクリアできれば,計算ができないという問題は解決に近づきそうです。
色そろばんはこの問題に対して,「テトリス」のようなアプローチをを取りました。例えば,7という数はsubitizingの視点で見ると,(5,2)の組み合わせで表現でき,この(5,2)をさらに,平面上で数種の表現ができるようにしました。これにより,すべての加法・減法をsubitizngの「組み合わせの変化」で表現できるようになりました
文章で書くと非常に複雑に見えますが,実際に動画で見ると,あなたがいつも使っている計算を平面上で表現しているにすぎないことに気づことでしょう。
色そろばんでの具体的な解決方法をご覧ください ▶使い方
色そろばんの学習効果は,著しいものでした。指を使っても計算を間違う学習者が色そろばんを使わずに,三桁の暗算ができるようになったのです。 ▶色そろばんの効果
なぜ,筆算学習をしても暗算ができないのか。
ピアジェの発達段階理論から考えてみる。
学校での計算指導は,筆算学習が主なものとなっています。学校以外での計算学習も筆算学習が計算学習となっています。
我々大人は,小学校での計算学習は筆算学習だったので違和感は感じないでしょう。 しかし,計算が苦手な人,障害等により計算ができない人にとって筆算学習は苦痛以外何物でもありません。筆算以外の学習方法はないものかと考えてしまいます。
そもそも,筆算で計算システムを学習することは,理にかなったものなのでしょうか。
スイスの心理学者ビアジェ(1986~1980)の発達段階理論から筆算学習を考えてみます。
発達段階理論は子供の発達を以下の4段階に分けて考えます。
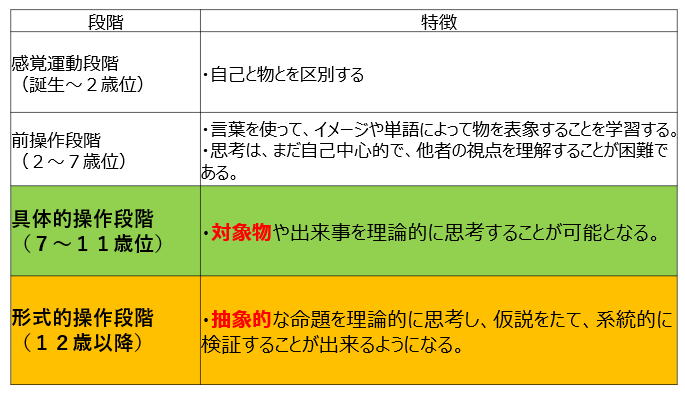
子供が学校で筆算が習う時期はその年齢から考えると,ピアジェの発達段階理論から見ると③の具体的操作期に該当します。抽象的な思考が苦手で,具体物及びその変化が思考の対象となっている時期です。計算に苦手意識があれば,具体物はより必要になります。
さて,筆算は具体物でしょうか?
紙と鉛筆で十進法システムを表現しているものなので具体物ではないでしょう。 つまり,本来ならば具体物で学習しなくてはいけない時期に抽象的なことを学習しているのです。
学習初期はブロック等を使って指導します。しかし,筆算の練習段階に入るとブロックは使いません。平均的な子供にとっては理解しにくいのは当たり前です。具体 操作期に形式的操作期の学習を強制しているからです。
この時期を頑張りぬいた人たちが形式的操作期に入り,やっと何が起きているのか理解ができるのです。
子供の時,筆算がなんだかわからなかったが大人になるとその意味が分かったということは多々あります。それは当然なことです。形式的操作期に入っているのですから。
なぜ,ほとんどの子供は筆算学習で躓くか理解できたと思います。
なぜ,計算学習を指導しても定着しないのか。
数の三項関係にピアジェの発達段階理論をブレンドさせて考えてみる。
数の三項関係とは,数を考えるとき,対象となる具体物があり,それを表現する話し言葉(数詞)があり,書き言葉(数字)がある。そして,これらはバラバラに存在しているのではなく,つながっているということを示している概念です。
これは,言われてみれば,当たり前のことです。
リンゴを想像してください。まず,「りんご」という書き言葉があります。これを読めば,読んでいる人は「RI NGO 」と発音します。おそらく,住んでいる人の地域ごとに発音のニュアンスは異なるでしょう。話し言葉の特性です。そして,これらの話し言葉,書き言葉の対象は甘酸っぱい味がするリンゴを意味しています。
我々が用いている言語は,我々の①「聴く・話す」と②「見る」に大きく依存します。①は話し言葉,②は書き言葉です。①と②が表したいもの「③対象」と考えれば,ここにも三項関係を見出すことができます。
ここから分かることは数の三項関係とは,数を一つの言葉として見た場合,一般的な言葉が持つ,①話し言葉・②書き言葉・③その対象,これらの①②③の属性を同じように持っいるということを言っているにすぎません。言い換えれば,数は言語の一部分であるということでしょう。
では,この数の三項関係を見ていきましょう。図示すれば,下図のようになります。
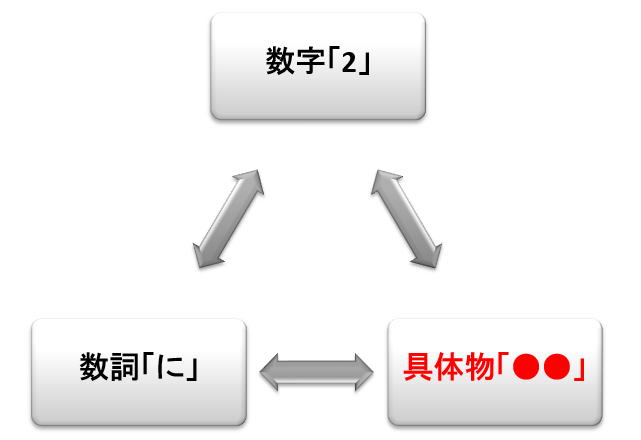
上図は「2」に関しての三項関係です。もし,リンゴであれば,具体物の欄にリンゴを書くのですが,単に「2」に関しての3項関係なので,具体物の欄には●を2個書きました。
数詞はいつ学習するのでしょうか? 小さいときを思い出してください。「あと,ジュゥ数えたらお風呂から上がりましょうね」と言われた方も多いと思います。数字の学習の前に一から十までの数詞は学習していると思います。そして,その数詞の意味も何となく理解が進んでいきます。多くの場合,この時期の三項関係の学習は自然に学習できたと思います。
そして,小学校に入ると足し算を学習します。これを三項関係の図を応用して示せば以下のようになるでしょう
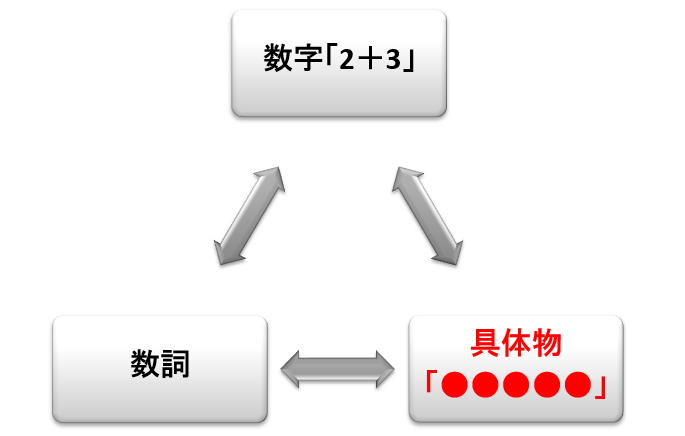
書き言葉は3+2です。先生は,足し算の意味を理解させるために,数字「3+2」,数詞「さんたすに」を具体物を使って指導してくれました。この時点では,一般的なクラスではほとんどの人が先生の説明を理解しています。
学習が進んでいくと,今度は足し算の繰り上がりを学習します。
繰り上がりの足し算も,数の三項関係から見てみると以下のようになるでしょう
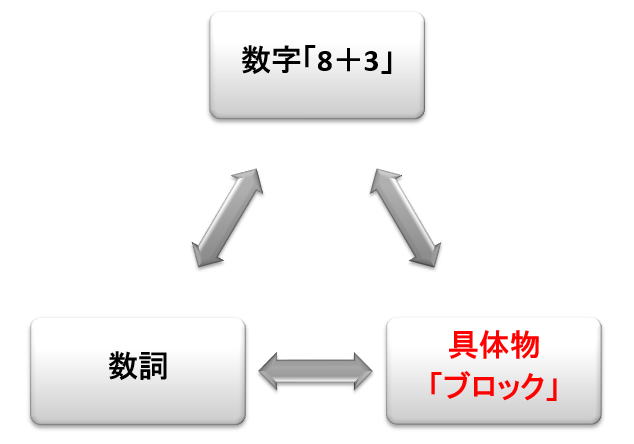
最初は,繰り上がりの意味を理解するために,ブロック等を使って学習します。しかし,すべての問題において,そのような具体的な操作をすることは,時間がかかり,ブロック等もバラバラになってしまうので,いつの間にか,紙の上で学習が完結するようになります。つまり,具体物が消えてきます。
いわゆる,「さくらんぼばなな」的な指導では具体物は消えていき,数の分解ができることが前提となります。
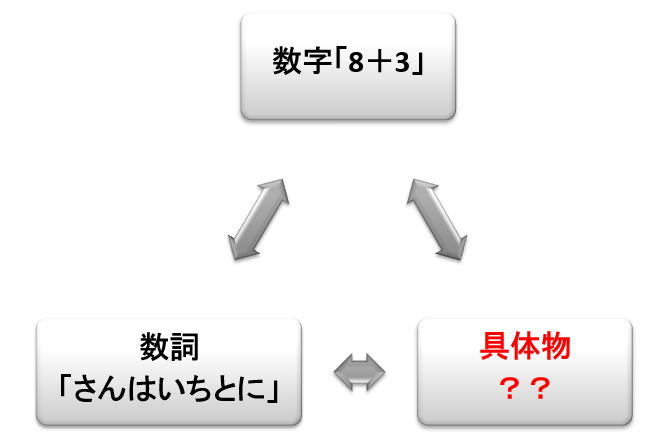
ここで,理解ができない学習者には何が起きているのでしょうか。おそらく,式は読めるけど,何を言っているのかわからないという状態ではないでしょうか。
その原因は簡単です。理解のための具体物がないのです。この段階では,ブロックは具体物としての機能を果たせるので,ブロックを用いて指導すべきです。
では,繰り下がりはどうすればいいのでしょうか。二位数,三位数の繰り下がりは具体物を使って教えることができるのでしょうか。
算数が苦手,計算が苦手な児童生徒に対しては,その指導において,具体物の必要性は高まります。IQの分布を前提に考えれば
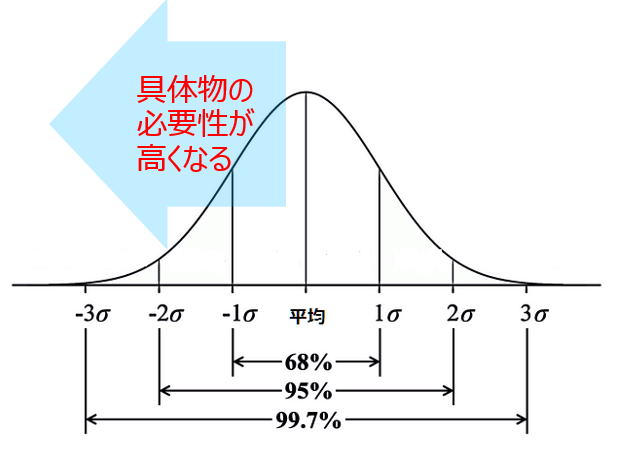
指導に際して,具体物の必要性が高いことは一目瞭然です。
理解が進んでいる児童生徒にとっては,具体物がなくても,形式的な次元で理解ができるので問題はないでしょう。しかし,理解するために,具体物が必要な児童生徒,すなわち,具体的操作段階にいる児童生徒にとっては,その理解のためには具体物が必要なのです。
この「具体物」を簡易に提供できるのが色そろばんなのです。
算数障害,計算障害の支援方法にも多様な議論があります。お金を使ったり,ゲームをしたり,pc,タブレットを使うなどの色々な方法が議論されています。しかし,最も大事なことは,学習に際して具体物を提供することなのです。
色そろばんの効果
多くの指導事例のうちの一部を紹介いたします。数感覚に基づいた暗算ができるようになるので,割り算,小数,分数への進むことができています。
以下は、実際の指導記録に基づくデータの一部です。
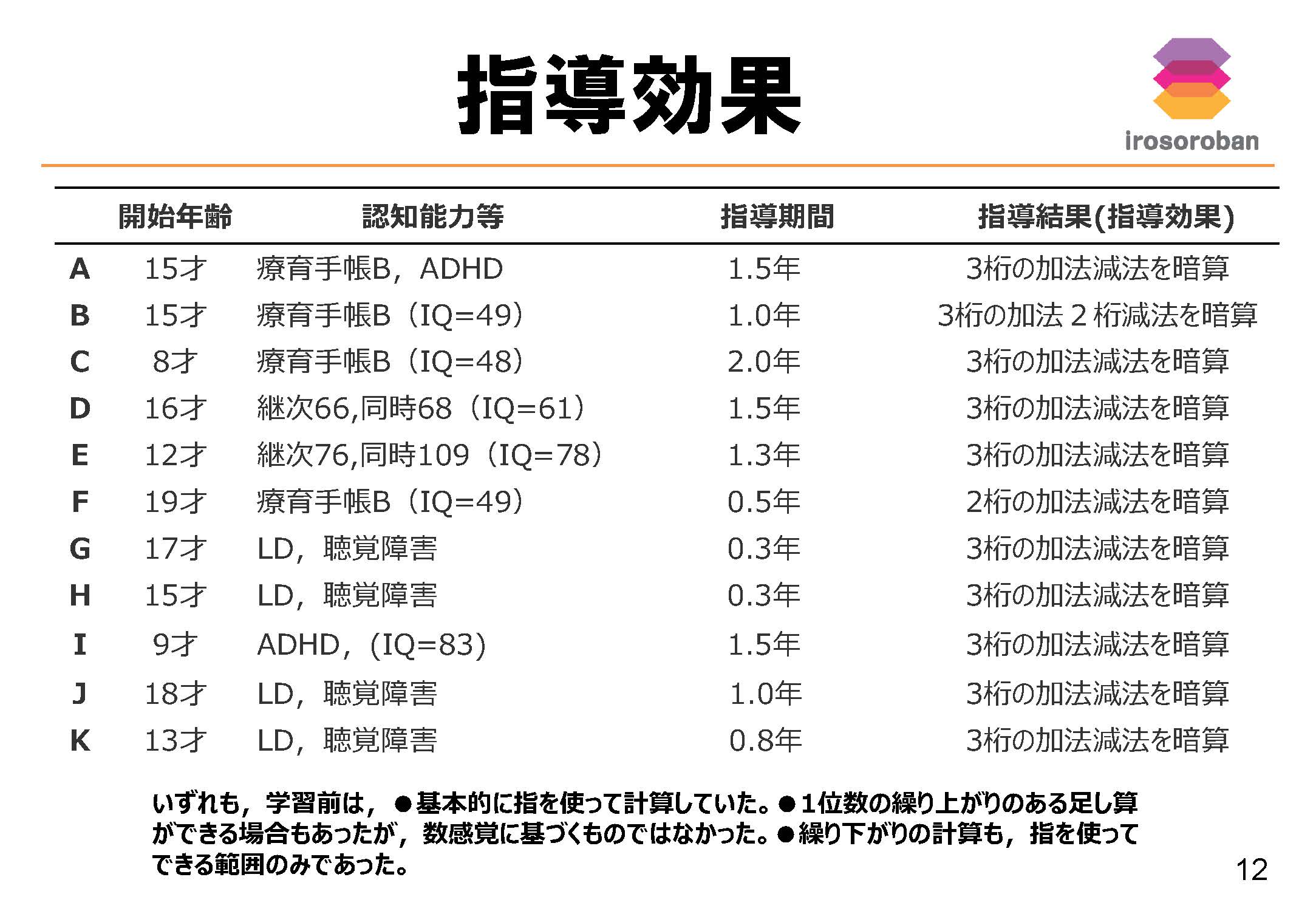
指導効果の具体的データ
■ 上記改善事例(画像)をテキストで説明します
- 15歳/療育手帳B・ADHD/1年6か月 → 3桁の加法・減法を暗算で処理可能
- 15歳/療育手帳B(IQ49)/1年 → 3桁加法・2桁減法を暗算習得
- 8歳/療育手帳B(IQ48)/2年 → 3桁加減算を暗算習得
- 16歳/IQ61/1年6か月 → 3桁加減算を暗算習得
- 12歳/IQ78/1年3か月 → 3桁加減算を暗算習得
- 19歳/療育手帳B(IQ49)/6か月 → 2桁加減算を暗算習得
- 17歳/LD・聴覚障害/3か月 → 3桁加減算を暗算習得
- 15歳/LD・聴覚障害/3か月 → 3桁加減算を暗算習得
- 9歳/ADHD(IQ83)/1年6か月 → 3桁加減算を暗算習得
- 18歳/LD・聴覚障害/1年 → 3桁加減算を暗算習得
- 13歳/LD・聴覚障害/10か月 → 3桁加減算を暗算習得
■ 指導前の共通課題
- 基本的に指を使って計算していた
- 1位数の繰り上がりが偶然できることはあったが、数概念理解に基づくものではなかった
- 繰り下がり計算は指で処理できる範囲に限定されていた
■ 成果の特徴
指導した11名のうち10名が、3桁の加減算を暗算で処理できる水準に到達しました。最短3か月で改善した事例もあります。療育手帳B、ADHD、LD、聴覚障害などの発達特性を持つ子どもでも、3か月〜2年の指導で計算力の向上が確認されています。学習前は指を使った計算のみでしたが、数概念を土台から再構築することで安定した暗算力が身につきました。年齢やIQに関わらず、数概念の理解が改善の鍵となっています。
保護者の方の感想
小学6年(ADHD,算数障害) 女児のお母さま
娘は現在小学6年生ですが,4年生に進級する頃に幸運にも色そろばんに出会い2年程学びました。計算が苦手で簡単な計算も指を使っていましたし,かけ算も6の段以降はつまづいていました。色そろばんを始めた当初は,使い方が一般的なそろばんとは異なり戸惑いもありましたが,徐々に数感覚が身に付き,色そろばん塾を卒業する頃には掛け算はもちろん三桁の計算なら暗算も出来るようになりました。短期間の劇的な成長に驚きました。また,色そろばんを続ける事により集中力も身に付きました。始めた当初は,計算を解く事が出来ずイライラして泣いてしまうことが多々あったのですが,数感覚を養い問題が解けるようになると,気持ちもコントロールする事が出来るようになり集中して取り組めるようになりました。娘にとって色そろばんで学んだことは,前に進むための大きな一歩となり大変嬉しく思っています。感謝の気持ちでいっぱいです。ありがとうございます。
30代 女性(算数障害)
私は長いこと算数障害に悩んでました。 どうして自分は繰り上がりのある足し算や引き算ができないのだろうとずっと悩み続けていました。小中学生の頃のテストは,他の科目の成績はそこそこよかったものの,数学だけは全滅でした。 ある時,インターネットで検索中に算数障害という言葉を知り,自分はそれじゃないかと疑い始めました。「色そろばん」を同じくネットで知りさっそく私も学習を始める決意ができました。 色そろばんの学習で嬉しかったこと・良かったことは,何よりも,いままでできなかったことができるようになったことです。努力すれば自分でもできるという自信がつきました。又,同じ算数障害に悩んでいる方々にも,色そろばんをお勧めしたいですね。 LINE学習でよかったことは,何よりもスキマ時間にできることです。また,分からないことや困ったことなどを気軽に質問できるからです。改めて学習を始めてよかったと思ってます。
小学1年 男児のお母さま
色そろばんをやり始め、毎日コツコツ取り組む学習の習慣がつきました。 定期的に学習状況を動画で確認しその都度気をつけるポイントを指導してもらえるので、指導に沿った計算方法が定着しました。子どもも色そろばんで自信がついたようで、嬉しく思います。
高校1年 男子(知的障害)のお母さま
色そろばんを日々取り組むことで数に対して苦手意識がなくなりました。集中力も身についたので計算が早くできるようになり,本人の自信にもつながってよかったと思います。(【補足】2年間の学習で,3桁の足し算・引き算及び2位数×1位数の掛け算を,色そろばんなしの暗算で計算できるようになり,その後,小数・分数の学習に進むことができた。)
小学2年女児 のお母さま
娘は算数が苦手で「数」というものを教えることが難しく何か良いものがないか?と探してたときに「色そろばん」と出会いました。私は子供の時に「そろばん」が難しく理解できないまま大人になったのですが、「色そろばん」は優しく簡単に出来そうに感じました。 実際やってみるとすごく簡単に操作、理解ができました。独学から娘にスタートさせてみましたが、やはり教えるにあたりつまずくことも多くLINE塾を受講することしました。 進め方。わからないこと。気になること。考えかた。どういうふうに子供と向き合っていくべきか。些細なことでもすぐに返答をいただけるのは助かっていますし、活力になります。LINE塾を受講して8ヶ月ほどたちましたが、娘も「数」に対して苦手意識が減り少しずつ計算力も上がってきています。 娘と一緒にやっていると私も考えなくても「数が見える」(サビタイジング)感覚があります。不思議な感覚で「これか!」と算数が楽しくなります。これが娘にも身についてくれると嬉しいです。 娘は毎日、学校へ行く前に頑張って取り組んでいます。色そろばんを操作して答えが出せて、「こうなるのか!」と実感できるのが楽しいと言っています。目、手、頭を使う色そろばんは子供に限らず大人の認知能力の向上にも役立っていると思います。日々の積み重ねが大切なので無理のない範囲で続けていきたいと思います。数ヶ月後、数年後にどれほど計算力が伸びているのか楽しみです。
関連情報
この記事の著者:渡部 敬(わたなべ けい)
色そろばん発明者 / 第14回 辰野千壽教育賞 優秀賞受賞
10年以上にわたる教育現場での実践に基づき、計算指導の画期的な新しい方法である「色そろばん」とその理論を発明。
【文科省研究事業】
文部科学省「特別支援教育に関する実践研究充実事業」2019, 2021, 2022において研究実践が採用・掲載。算数学習に困難を抱える児童生徒への有効な指導法として、公的な教育データベースに記録されています。
【国立大学からの表彰】
国立大学法人上越教育大学より「第14回 辰野千壽教育賞」優秀賞を受賞。サビタイジング理論を応用した独自の指導体系は、教育実践研究の典型として高く評価されています。

第14回辰野千壽教育賞 優秀賞 授与式にて。中央が発明者の渡部敬