繰り上がり・繰り下がりができない理由
足し算・引き算、特にに繰り上がり・繰り下がりができない原因は、単なる練習不足ではありません。数概念の理解が不十分なまま計算手順だけを覚えようとすると計算は安定しません。

上の画像は、IQ=78でADHD、学習障害のある中学1年生男子の事例です。学習期間は1年半でした。指導前と指導後の実際の変化を示しています。数概念を土台から再構築することで、3桁の加減算が暗算で処理できるようになりました。この改善は単なる反復練習ではなく、概念理解の支援によって生じたものです。当初は指を使っても100マス計算に20分かかっていましたが、色そろばんの指導後は3分42秒で解けるようになりました。
足し算ができない、引き算ができない、指を使わないと不安、数を1つずつ数え直す、「あといくつで10」が瞬時に出ない、何度教えても定着しない……。繰り上がり・繰り下がりができない等の原因は、単なる計算練習不足ではありません。数概念の弱さが影響している場合があります。本ページでは具体的な改善事例と指導方法を解説します。
このページでは、人が生まれながら持っている数概念(サビタイジング)に視点を当てて解説します。
繰り上がり・繰り下がりの困難には複数の要因が指摘されていますが、その中でも『数概念(subitizing)』の弱さは、共通して見られる重要な要因の一つです。当サイトでは、これらを一つの一貫した認知的視点から整理し、体系的にアプローチします。
タブレットでの反復練習やスモールステップだけでは、十分に理解が深まらない場合もあります。それを、色そろばんは、視覚的に数のまとまりを再構築し、数概念の理解を促します。
この問題を解決するキーワードが「subitizing(サビタイジング)」であることは、「なぜ計算ができないのか」のページでご説明のとおりです。
繰り上がりが難しい背景の一つとして、subitizingの組み合わせという視点が関係している可能性があります。
Subitizingの組み合わせとは?
1992年、科学誌『Nature』において、生後5か月の乳児が数量の変化に対して予測を持つことを示した研究が報告されました(Wynn, 1992)。この研究は、人間が生得的な数認知能力を持つ可能性を示唆しています。
言語を理解しない段階の乳児でも、数量の変化に一定の予測を示すことが報告されています。これらの研究は、人間が生得的な数認知能力を持つ可能性を示唆しており、その応用として組み合わせによる認知も考えられています。
一般に、subitizingは4~5程度までと報告されていますが、例えば「6」という数は、「1」のsubitizingと「5」のsubitizingの組み合わせとして認知していると考えられます。この考え方は、古代文明の記数法にも見られます。

このように、subitizingの範囲は5までですが、組み合わせることにより5より大きい数も直感的に認知できるのです。
2~10までの数をsubitizingの組み合わせで表現すると、以下のようになります。
3.jpg)
この考え方に立つと、計算とは「subitizingの組み合わせを変化させること」と捉えることができます。
なぜ繰り上がり・繰り下がりができないのか
ここで、繰り上がりのある「8+3」の計算を考察します。一般的な指導法(さくらんぼ計算など)では、「10の補数(あといくつで10になるか)」を考え、数を分解して計算します。しかし、算数の苦手な子は、まずこの説明自体が理解できません。
指導の目的は「補数」という考え方を習得させることですが、苦手な子は「数え上げ(カウンティング)」で乗り切ろうとします。ここに繰り上がりでつまずきやすい一因があると考えられます。
カウンティングだけに頼らず、subitizingを活用する視点を取り入れることで、理解が進みやすくなる場合があります。
色そろばんによる解決策
色そろばんは、subitizingの組み合わせを視覚的に捉えやすくする教材の一つであり、繰り上がり・繰り下がりの理解を助ける場合があります。
下図の仕組みにより、数をsubitizingの組み合わせで認知できるようになります。

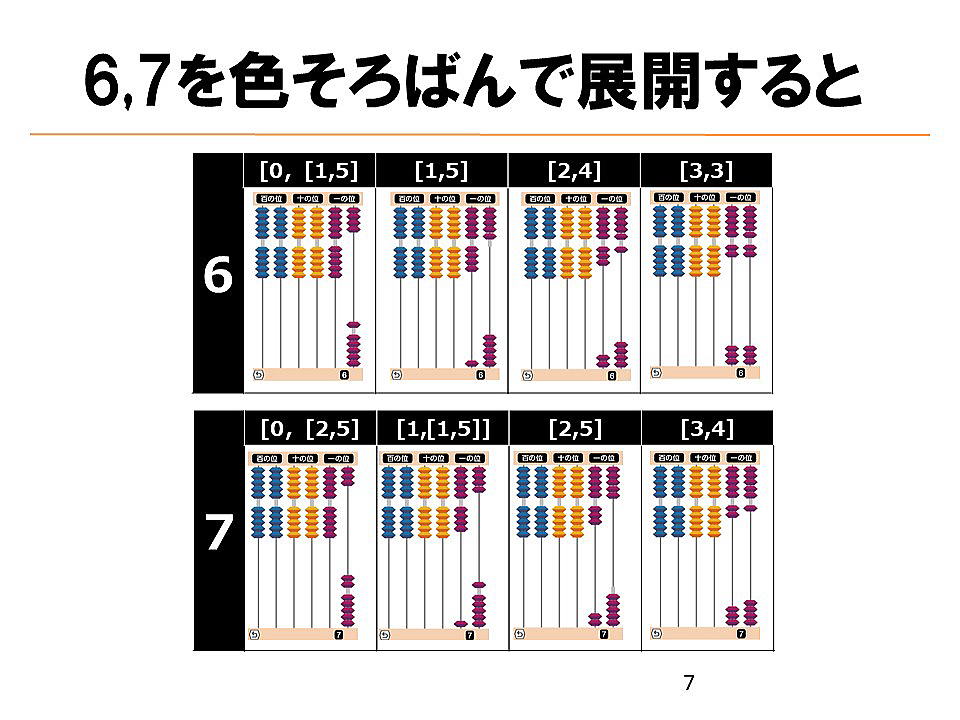
繰り上がりの足し算も、下図のようにsubitizingの組み合わせとして視覚的に理解しやすくなります。

学習用動画で確認すると、より容易に理解できるでしょう。
2位数+2位数(繰り上がりが2回あり)の足し算も、色そろばんを使えば動画のように理解しやすくなります。
繰り下がりでよくある「17-8=11」のような間違い(引けないから大きい方から引いてしまう)も、色そろばんで学習すれば視覚的に理解しやすくなります。

「102-3」,「655-457」等、3位数の繰り下がりがある引き算も、色そろばんを使えば理解しやすくなります。↓の動画をご覧ください
既存の指導法との比較
難しい「補数」の概念を後回しにできる
繰り上がりの計算では補数を学びますが、計算が苦手な子は結局カウンティングで答えを探し、文章問題の意味が理解できなければ先に進めません。この段階では必ずしも先に学ぶ必要はありません。難しい補数の勉強は後回しです。補数は色そろばんの操作を体験することにより自然に理解できるからです。
さくらんぼ計算で混乱する子も、色そろばんでは迷いません
一般的な指導法では、補数を見つけた後に数を分解して10の塊を作りますが、手数が増え混乱の原因になります。玉の操作が中心となるため、手順が整理しやすいと感じる子どももいます。
減加法のような複雑なステップを踏まずに計算できる
繰り下がりの引き算で使われる減加法は、「引き算なのになぜ足し算するの?」という疑問を生みやすく、子どもを混乱させます。色そろばんでは複雑な手順をできるだけ減らすことができます。subitizingできる数のまとまりとして玉を捉えるため、補数操作に頼らず理解しやすくなります。
でも、色そろばんで「筆算」を見ると、意味が非常にクリアになる
色そろばんは新しい指導方法です。既存の指導方法で色そろばんを使うと色そろばん本来の効果が薄れます。しかし、現行の指導方法を、色そろばんで見ることにより、その意味を明らかにすることができます。色そろばんはsubitizingの組み合わせを変化させるという認知レベルでの学習を可能にさせているからできるのです。筆算は『手順』の暗記になりがちですが、色そろばんは筆算の『意味』を可視化します。玉の操作が筆算の繰り上がりの意味と対応しているため、理解が結びつきやすくなります。認知レベルで筆算を見てみましょう。
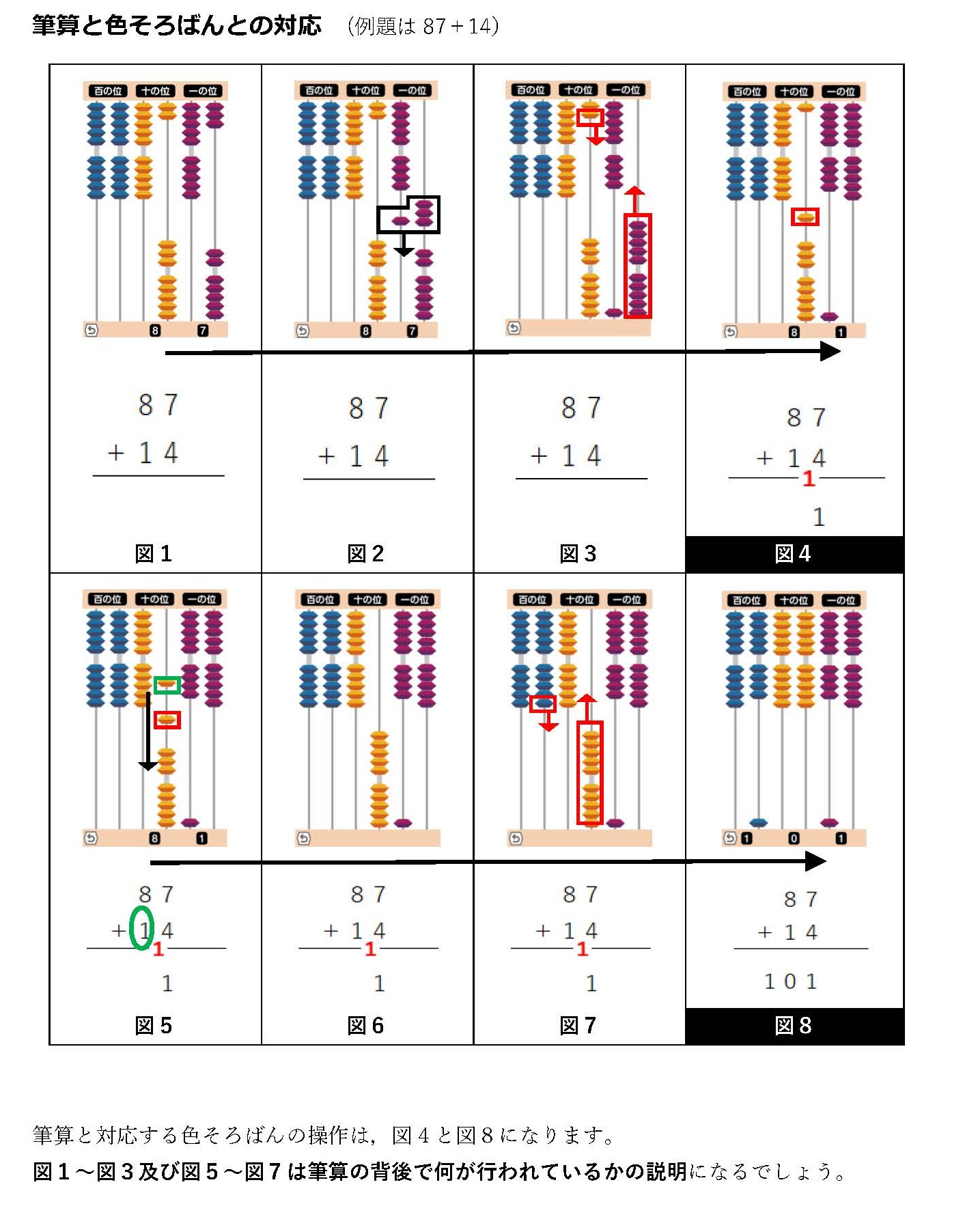
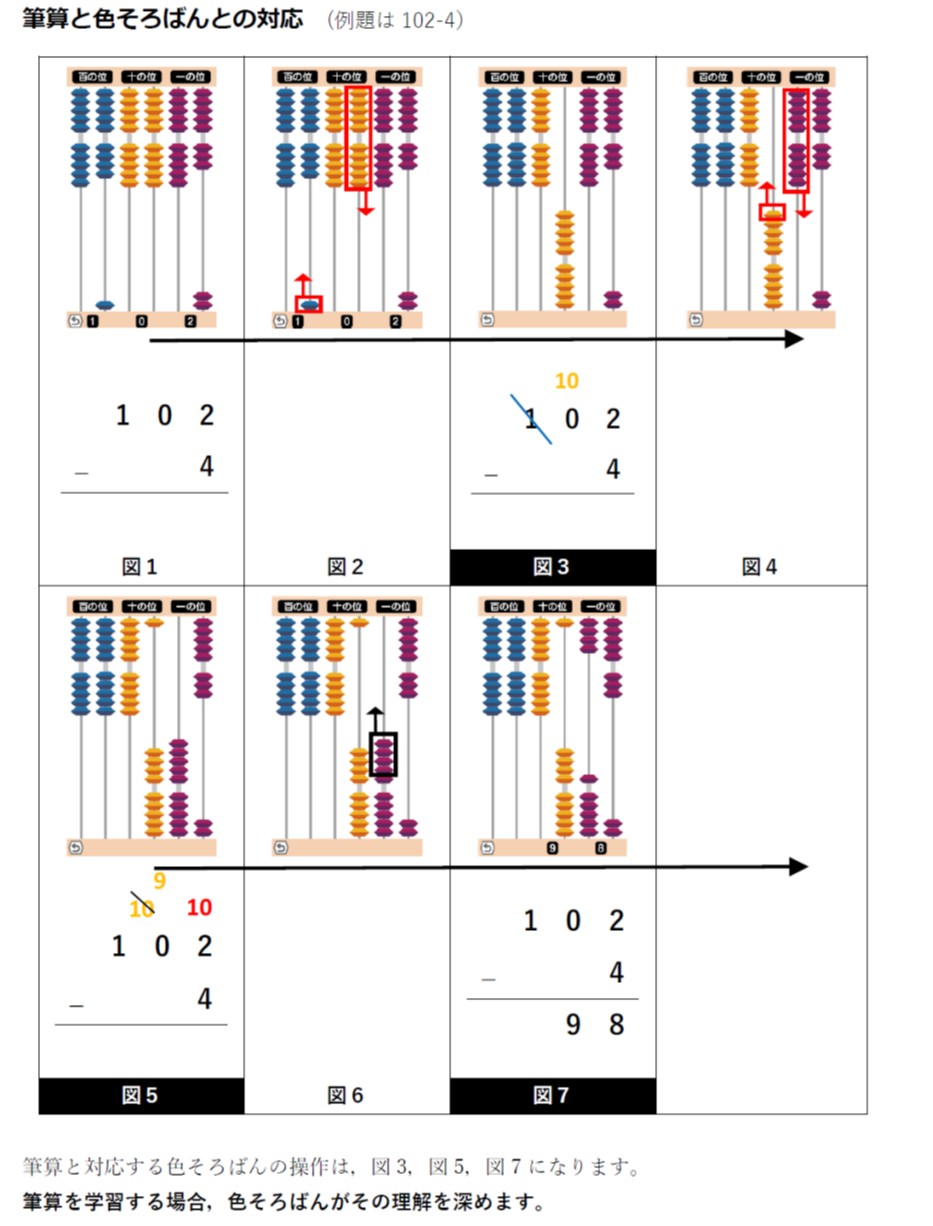
ご覧のように色そろばんの学習で求められるのは,人が本来持っているsubitizingです。主に言語理解に依存しない形で学習を進められます。また,補数を求めるように,物事を逆に考える必要もありません。こうした理解の積み重ねが、計算への自信につながるケースも見られます。つまり,色そろばんの玉の動きは十進法の思考そのものを表しており,この具体物に習熟することにより抽象的な十進法の思考が頭の中に自然にできるのです。計算への不安が軽減し、前向きに取り組めるようになる事例も報告されています。
色そろばんの効果
多くの指導事例のうちの一部を紹介いたします。数感覚に基づいた暗算ができるようになるので,割り算,小数,分数への進むことができています。
以下は、実際の指導記録に基づくデータの一部です。
指導効果の具体的データ
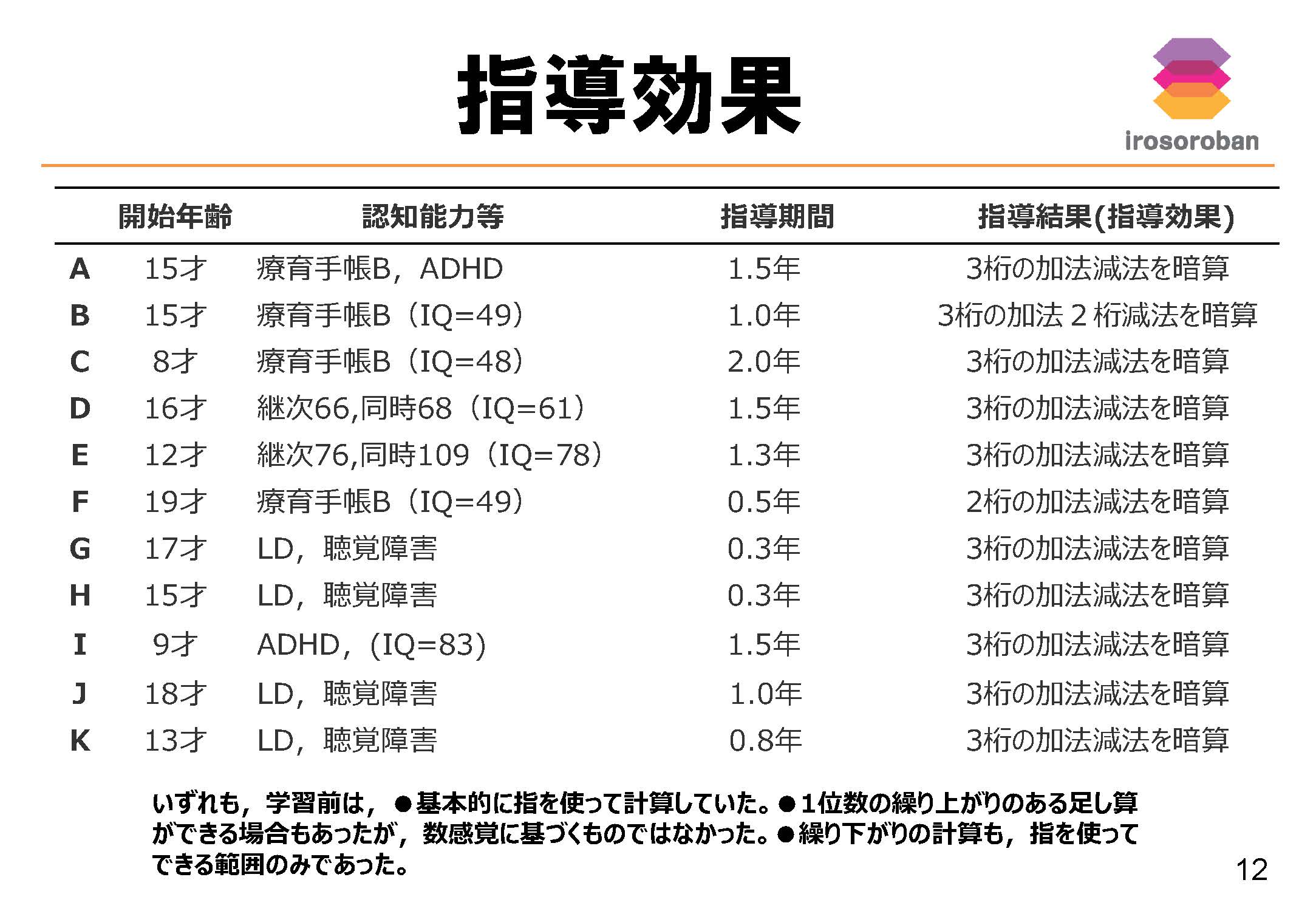
■ 上記改善事例(画像)をテキストで説明します
- 15歳/療育手帳B・ADHD/1年6か月 → 3桁の加法・減法を暗算で処理可能
- 15歳/療育手帳B(IQ49)/1年 → 3桁加法・2桁減法を暗算習得
- 8歳/療育手帳B(IQ48)/2年 → 3桁加減算を暗算習得
- 16歳/IQ61/1年6か月 → 3桁加減算を暗算習得
- 12歳/IQ78/1年3か月 → 3桁加減算を暗算習得
- 19歳/療育手帳B(IQ49)/6か月 → 2桁加減算を暗算習得
- 17歳/LD・聴覚障害/3か月 → 3桁加減算を暗算習得
- 15歳/LD・聴覚障害/3か月 → 3桁加減算を暗算習得
- 9歳/ADHD(IQ83)/1年6か月 → 3桁加減算を暗算習得
- 18歳/LD・聴覚障害/1年 → 3桁加減算を暗算習得
- 13歳/LD・聴覚障害/10か月 → 3桁加減算を暗算習得
■ 指導前の共通課題
- 基本的に指を使って計算していた
- 1位数の繰り上がりが偶然できることはあったが、数概念理解に基づくものではなかった
- 繰り下がり計算は指で処理できる範囲に限定されていた
■ 成果の特徴
指導した11名のうち10名が、3桁の加減算を暗算で処理できる水準に到達しました。最短3か月で改善した事例もあります。療育手帳B、ADHD、LD、聴覚障害などの発達特性を持つ子どもでも、3か月〜2年の指導で計算力の向上が確認されています。学習前は指を使った計算のみでしたが、数概念を土台から再構築することで安定した暗算力が身につきました。年齢やIQに関わらず、数概念の理解が改善の鍵となっています。
保護者の方の感想
小学6年(ADHD,算数障害) 女児のお母さま
娘は現在小学6年生ですが,4年生に進級する頃に幸運にも色そろばんに出会い2年程学びました。計算が苦手で簡単な計算も指を使っていましたし,かけ算も6の段以降はつまづいていました。色そろばんを始めた当初は,使い方が一般的なそろばんとは異なり戸惑いもありましたが,徐々に数感覚が身に付き,色そろばん塾を卒業する頃には掛け算はもちろん三桁の計算なら暗算も出来るようになりました。短期間の劇的な成長に驚きました。また,色そろばんを続ける事により集中力も身に付きました。始めた当初は,計算を解く事が出来ずイライラして泣いてしまうことが多々あったのですが,数感覚を養い問題が解けるようになると,気持ちもコントロールする事が出来るようになり集中して取り組めるようになりました。娘にとって色そろばんで学んだことは,前に進むための大きな一歩となり大変嬉しく思っています。感謝の気持ちでいっぱいです。ありがとうございます。
30代 女性(算数障害)
私は長いこと算数障害に悩んでました。 どうして自分は繰り上がりのある足し算や引き算ができないのだろうとずっと悩み続けていました。小中学生の頃のテストは,他の科目の成績はそこそこよかったものの,数学だけは全滅でした。 ある時,インターネットで検索中に算数障害という言葉を知り,自分はそれじゃないかと疑い始めました。「色そろばん」を同じくネットで知りさっそく私も学習を始める決意ができました。 色そろばんの学習で嬉しかったこと・良かったことは,何よりも,いままでできなかったことができるようになったことです。努力すれば自分でもできるという自信がつきました。又,同じ算数障害に悩んでいる方々にも,色そろばんをお勧めしたいですね。 LINE学習でよかったことは,何よりもスキマ時間にできることです。また,分からないことや困ったことなどを気軽に質問できるからです。改めて学習を始めてよかったと思ってます。
小学1年 男児のお母さま
色そろばんをやり始め、毎日コツコツ取り組む学習の習慣がつきました。 定期的に学習状況を動画で確認しその都度気をつけるポイントを指導してもらえるので、指導に沿った計算方法が定着しました。子どもも色そろばんで自信がついたようで、嬉しく思います。
高校1年 男子(知的障害)のお母さま
色そろばんを日々取り組むことで数に対して苦手意識がなくなりました。集中力も身についたので計算が早くできるようになり,本人の自信にもつながってよかったと思います。(【補足】2年間の学習で,3桁の足し算・引き算及び2位数×1位数の掛け算を,色そろばんなしの暗算で計算できるようになり,その後,小数・分数の学習に進むことができた。)
小学2年女児 のお母さま
娘は算数が苦手で「数」というものを教えることが難しく何か良いものがないか?と探してたときに「色そろばん」と出会いました。私は子供の時に「そろばん」が難しく理解できないまま大人になったのですが、「色そろばん」は優しく簡単に出来そうに感じました。 実際やってみるとすごく簡単に操作、理解ができました。独学から娘にスタートさせてみましたが、やはり教えるにあたりつまずくことも多くLINE塾を受講することしました。 進め方。わからないこと。気になること。考えかた。どういうふうに子供と向き合っていくべきか。些細なことでもすぐに返答をいただけるのは助かっていますし、活力になります。LINE塾を受講して8ヶ月ほどたちましたが、娘も「数」に対して苦手意識が減り少しずつ計算力も上がってきています。 娘と一緒にやっていると私も考えなくても「数が見える」(サビタイジング)感覚があります。不思議な感覚で「これか!」と算数が楽しくなります。これが娘にも身についてくれると嬉しいです。 娘は毎日、学校へ行く前に頑張って取り組んでいます。色そろばんを操作して答えが出せて、「こうなるのか!」と実感できるのが楽しいと言っています。目、手、頭を使う色そろばんは子供に限らず大人の認知能力の向上にも役立っていると思います。日々の積み重ねが大切なので無理のない範囲で続けていきたいと思います。数ヶ月後、数年後にどれほど計算力が伸びているのか楽しみです。
関連情報
この記事の著者:渡部 敬(わたなべ けい)
色そろばん発明者 / 第14回 辰野千壽教育賞 優秀賞受賞
10年以上にわたる教育現場での実践に基づき、計算指導の画期的な新しい方法である「色そろばん」とその理論を発明。
【文科省研究事業】
文部科学省「特別支援教育に関する実践研究充実事業」2019, 2021, 2022において研究実践が採用・掲載。算数学習に困難を抱える児童生徒への有効な指導法として、公的な教育データベースに記録されています。
【国立大学からの表彰】
国立大学法人上越教育大学より「第14回 辰野千壽教育賞」優秀賞を受賞。サビタイジング理論を応用した独自の指導体系は、教育実践研究の典型として高く評価されています。

第14回辰野千壽教育賞 優秀賞 授与式にて。中央が発明者の渡部敬